Hello. This is the second entry in a series documenting the development of my graphical programming environment, Game Painter.
In my first entry, I talked about the front end to various rule forms, and today I wanted to follow it up with a discussion of the back end.
Cellular Automata as look-up tables
The goal of Game Painter was to make a graphical programming interface, so as I was thinking about what made sense for the UI, I happened to stumble on a chapter of Daniel Shiffman’s The Nature of Code about cellular automata. The diagrams in the chapter helped me see that the logic of cellular automata has a strong graphical interpretation. Cellular automata could be defined graphically!
This graphical interface would need to be supported by some sort of back end implementation. The first back-end solution came from that same chapter from the Nature of Code. Here’s the basic idea:
In Stephen Wolfram’s concept of “elementary cellular automata,” cellular automata are encoded as strings of digits. For example, if we take the following rule diagram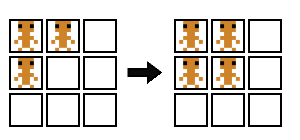
We can assign digits to each unique sprite and form two numbers, one on the left-hand side and one on the right-hand side. 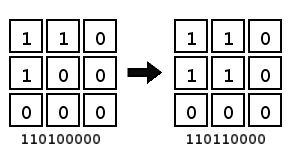
That’s 110100000 and 110110000 in binary, or 416 and 432 in decimal. But on the right-hand side, the center cell is the only one we care about because it’s the only one that changes state from left to right. So then we get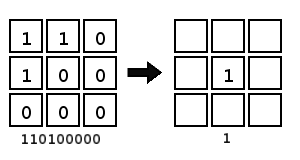
We can use the left number as an index to an array and use the right number as the value at that index.
var index = unbinary("110100000"); // index is assigned the value 416
var val = 1;
lookUpTable[index] = val;
We can compose all of our rules into a single table by writing them in sequence to the look-up table. This implies a prioritization of some rules over others because later rules in the sequence can overwrite earlier ones.
This procedure works generally for any number of unique sprites. If we have two unique sprites we can encode rules as binary numbers, if we have three unique sprites we can encode rules as trinary numbers, and so on and so forth. Finally, we can perform this encoding procedure on rules with any number of total sprites. That number becomes the number of digits in the encoding.
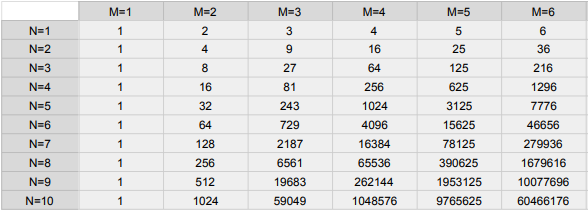
The advantage of this approach is that array lookup is instantaneous. But there is a serious limitation here. With N unique sprites and M total sprites, the size of the lookup table becomes M^N. This is fine for small rulesets such as Conway’s Game of Life (2^9 == 512) but quickly becomes problematic as rulesets become larger. This table shows how rapidly the array size grows as N and M grow.
One-to-one rule interpretation
Look-up tables proved not to be a good general solution, and the front-end was evolving in ways that were moving farther away from cellular automata. At this point, it seemed more natural to write a back-end implementation that reflected what was happening on the front-end more directly.
We define a general rule interface:
interface Rule
{
evalCell: (lvl: Level, i: number, j: number) => number;
}
Where i and j are the coordinates of the cell to evaluate in the given level.
We can implement a concrete Rule type for every form of rule, and there are many advantages to this approach.
With this solution, we have total flexibility to grow our language to incorporate new rule forms without affecting existing rule forms.
We can compose rules, defining them hierarchically, kind of like an abstract syntax tree. Except our tree is comprised of rules rather than expressions.
This solution is also conceptually simple. It provides a one-to-one relationship between the front-end and the back-end, and it enables a divide-and-conquer approach to implementation.
We can even fold our look-up table solution into this more general solution and use look-up tables in special cases. Look-up tables can be defined as a type of Rule. Something like this:
class LookUpTable implements Rule
{
private table: number[];
public evalCell(lvl: Level, i: number, j: number)
{
let index = parse(lvl, i, j); // get the neighborhood encoding
return table[index];
}
}
Until Next Time
For the next post, I plan on taking a break from these technically-oriented posts to talk about the high-level design ideas behind Game Painter. Stay tuned to this blog or follow me on Twitter @objstothinkwith to see more. Thanks for reading!